BFPRT

1. 概念

用于解决TopK问题。

• TopK问题：从长度为N的无序数组中找出前K大的数
• BFPRT算法：1973年，由5位科学家 Blum 、 Floyd 、 Pratt 、 Rivest 、 Tarjan发表了一篇 “Time bounds for selection” 的论文，讲述了如何选取第K大的元素，也称为”Median of medians”，即中位数的中位数算法。该算法的时间复杂度可以严格收敛到O(n)级别。

2. 实现原理

假设现在存在一个函数 GetKthNum(arr[], k) 可以获取到第k大的数，这个函数中要做哪些事情：

• 数组的长度为n，则每5个划分为1组，不够5个元素的单独成组，一共由n/5组。时间复杂度：O(1)
• 每5个数在组内排序，组与组之间无序。时间复杂度：O(1) * n / 5 = O(n)
• 将排好序的每组中的上中位数取出来单独成组MediansArr，该组的长度为n/5。然后递归的调用GetKthNum(MediansArr, n/10) 函数，目的是为了获取到中位数数组的中位数Pivot。
  • 上中位数：（1，2，3，4，5）取3，（1，2，3，4）取2
  • 为什么是n/10，因为数组的长度是n/5，其中位数的一定是处于n/10的位置。
  • 时间复杂度：自己调用自己，T(n/5)
• 此时用Pivot去进行快排中提到的 partition 过程，时间复杂度：O(n)
  • < Pivot 的数放在左边
  • = Pivot 的数放在中间

  • Pivot 的数放在右边

  将返回的等于区域数组pArr，判断是否命中K
  • pArr[0] == K，停止
  • pArr[0] > K，左半部分进行递归
  • pArr[0] < K，右半部分进行递归
• 上面的递归过程每次都可以严格的淘汰掉至少n*3/10的数据量，看图很容易明白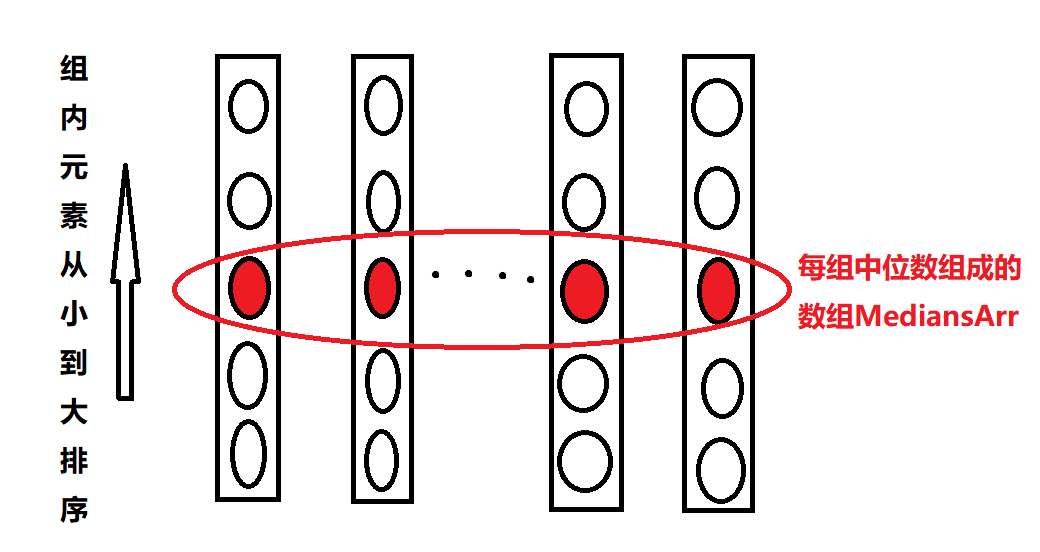： 一共有n/5组，中位数数组的中位数值为Pivot，在该数组中有n/10个数的值比Pivot小，这些数字在各自的小数组中又是中位数，则表示这些组每组存在3/5个数比Pivot小，所以在原数组中就至少有n*3/10的数据量比Pivot小。也就是最多n*7/10有比Pivot大，确定了递归规模。
• 整体时间复杂度T(n) = T(n/5) + T(n*7/10) + O(n)，可以收敛到O(n)，证明（参考链接）如下：

3. 代码实现

3.1 Partition过程回顾

vector partition(int arr[], int l, int r, int pivot) {
    vector<int> equals;
    int less = l - 1;
    int more = r;
    int m = l;
    while (m <= more) {
        if (arr[m] == pivot) {
            m++;
        }
        else if (arr[m] > pivot) {
            swap(arr[more--], arr[m]);
        }
        else if (arr[m] < pivot) {
            swap(arr[++less], arr[m++]);
        }
    }
    equals.push_back(less + 1);
    equals.push_back(more);
    return equals;
}

3.2 BFPRT实现

int* get_min_kth_nums_by_bfprt(int arr[], int len, int k)
{
    if (k < 1 || k > len)   return NULL;
    int kth_num_val = get_indexth_num_of_arr(arr, 0, len - 1, k - 1);
    int* res = new int[k];
    int ik = 0;
    for (int i = 0; i < len; ++i){
        if (arr[i] <= kth_num_val)
        {
            res[ik++] = arr[i];
        }
    }
    return res; 
}

int get_indexth_num_of_arr(int arr[], int l, int r, int index)
{
    if (l == r) return arr[l];
    int p = get_median_of_medians_arr(arr, l, r);
    // cout << "------------p------------" << p << endl;
    int* part_res = partition(arr, l, r, p);
    // cout << "part_res [0] = " << part_res[0] << ", part_res[1] = " << part_res[1] << endl;
    if (index >= part_res[0] && index <= part_res[1]){
        return arr[index];
    }else if (index < part_res[0]){
        return get_indexth_num_of_arr(arr, l, part_res[0] - 1, index);
    }else{
        return get_indexth_num_of_arr(arr, part_res[1] + 1, r, index);
    }
}

int* partition(int arr[], int l, int r, int p)
{
    int less = l - 1;
    int more = r;
    int i = l;
    while (i <= more){
        if (arr[i] < p){
            swap(arr[++less], arr[i++]);
        }else if (arr[i] > p){
            swap(arr[more--], arr[i]);
        }else{
            i++;
        }
    }
    int *part = new int[2];
    part[0] = less + 1;
    part[1] = more;
    return part;
}

int get_median_of_medians_arr(int arr[], int l, int r)
{
    int count = r - l + 1;
    // cout << "count: " << count << endl;
    int offset = count % 5 == 0 ? 0 : 1;
    int medians_arr_len = count / 5 + offset;
    // cout << "medians_arr_len: " << medians_arr_len << endl;
    int medians_arr[medians_arr_len];

    for (int i = 0; i < medians_arr_len; ++i){
        int part_begin = l + 5 * i;
        int part_end = min((part_begin + 4), r);
        medians_arr[i] = get_median(arr, part_begin, part_end);
    }
    /*
    cout << "medians_arr has: ";
    for (int i = 0; i <  medians_arr_len; ++i){
        cout << medians_arr[i] << " ";
    }
    cout << endl;
    */
    return get_indexth_num_of_arr(medians_arr, 0, medians_arr_len - 1, medians_arr_len / 2);
}

int get_median(int arr[], int l, int r)
{
    // 1. insert sort 
    insert_sort(arr, l, r);
    int mid = l + (r - l) / 2;
    // 2. return arr[mid]
    return arr[mid];
}

void insert_sort(int arr[], int l, int r)
{
    for (int i = l + 1; i <= r; ++i)
    {
        for (int j = i; j > l; --j)
        {
           if (arr[j] < arr[j - 1])
           {
               swap(arr[j], arr[j - 1]);
           } 
        }
    }
}