Manacher
2021-10-03 / ryanxw

Manacher

1. 概念

用于求取字符串中最大的回文子串，需要考虑的是奇回文 or 偶回文

  • 奇回文：123a321，其中字符a所处的位置为对称轴，实轴
  • 偶回文：1221，其中两个2中间的位置为对称轴，虚轴

所以在判断回文串时需要先处理一下字符串本身，让虚轴显示出来，比如加入特殊字符”#”来保证虚轴可以看到。

  • 不用担心特殊字符和字符串中的原字符发生冲突，因为是对称的，虚轴只会和虚轴相比较。
  • 处理过后的样子：
    • 奇回文：#1#2#3#a#3#2#1#
    • 偶回文：#1#2#2#1#

2. 实现原理

2.1 暴力解法

假设字符串的长度是N，处理成特殊字符后每个位置都开始向两边扩，比较字符，记录好最大的回文长度就ok，每次有更大的就更新。

  • 时间复杂度O(N^2)

2.2 manancher解法

解决掉在暴力解法中一些地方无需尝试扩，比较，直接向后跳即可。

几个概念

要先熟悉几个概念

  • 回文半径
  • 最右回文边界R（R一定停在特殊字符上，因为只有实际字符才存在不同，扩不动的情况）
  • 最有回文边界的中心C（只记录第一次【即最早】冲到R时候的C的位置，此时为最长情况）

几种拓扑图（核心）

初始化遍历字符串的下标 Index = 0

  1. 最右回文边界 R 在 Index 的左边，即 R < Index 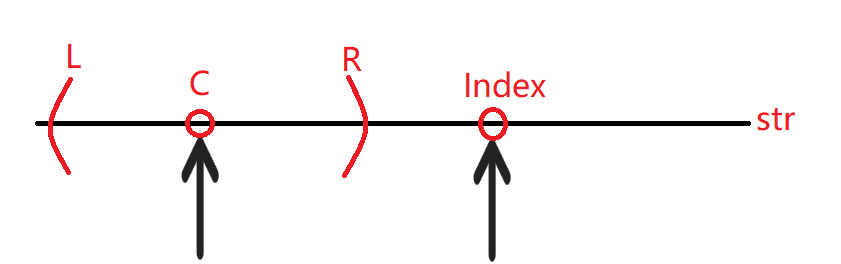Untitled 这种情况下没有优化空间，只能暴力匹配
  2. 最右回文边界 R 在 Index 的右边，即 R > Index
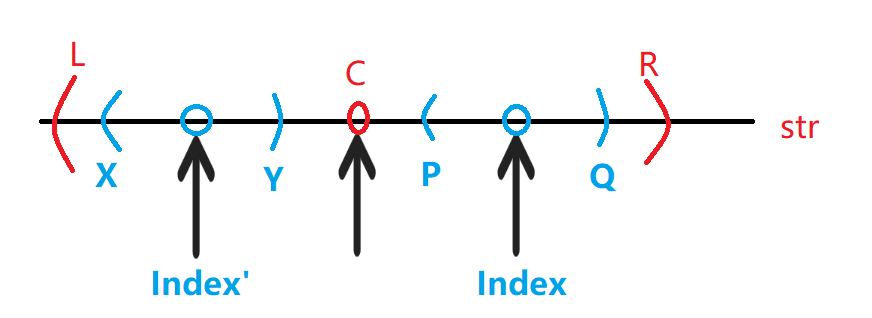
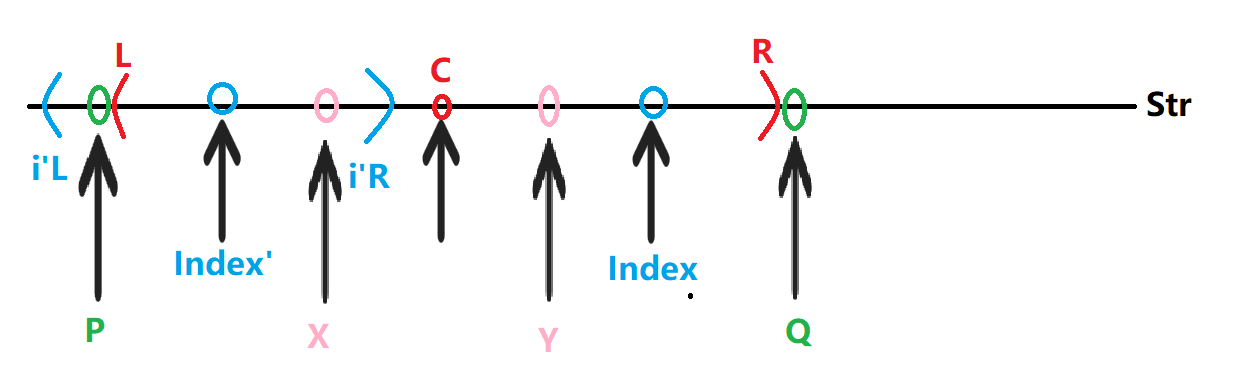
    1. Index 位置的对称点 Index’ 的回文范围就在 (L，R) 内 Untitled Untitled 由图可以知道在对称点 Index’ 的位置已经扩到了 X ≠ Y 处不能再向两边扩了。而目前Center所处的位置 C 所扩到最大的边界时（L，R），所以 P == Y, Q == X。而 X ≠ Y，则 P ≠ Q
    2. Index位置的对称点 Index’ 的回文范围只有部分在 (L，R) 内 Untitled Untitled 此时Index能扩充的范围就是（Index，R）。原因：
      • 由图可知目前 Center 所处的位置 C 所扩到最大的边界时（L，R），所以 P ≠ Q。
      • 而P在（i’L，i’R）这个当时以 Index’ 为中心的回文串中，则一定有一个 X 和 P 关于Index’ 对称，即 P == X
      • X 又在以 C 为中心的回文串（L，R）中，则必存在一个 Y 和 X 关于 C 对称，即X == Y
      • 因为 P == X，X == Y，所以 P == Y，而 P ≠ Q，则Y≠Q，所以最多扩到（Index，R）
      为什么（Index，R）就一定是回文呢？
      • 因为关于C对称
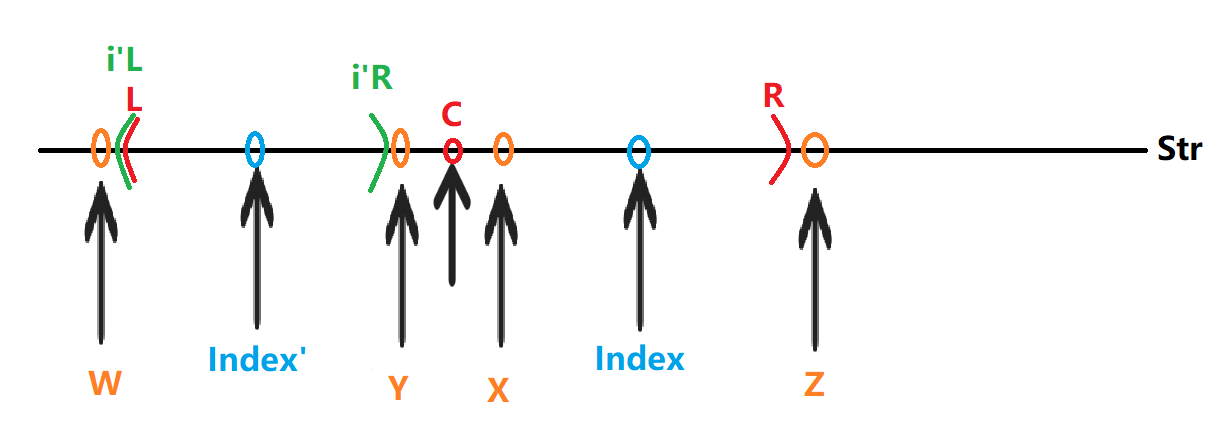
    3. Index位置的对称点 Index’ 的回文范围 (i’L，i’R) 中的 i’L 刚好和 (L，R) 的L重合 Untitled Untitled 由图可以知道 ：
      • X == Y
      • W ≠ Y，则 W ≠ X
      • W ≠ Z
      • 但是无法确认Z是否等于X，则只能暴力扩展去判断

总结分析

  • case1：i 在 R 右面，暴力扩，i增长，时间复杂度O(n)
  • case2：（i’L，i’R）在L内，不用扩，O(1)
  • case3：（i’L，i’R）部分在L内，即 i’L < L < i’R < R，不用扩，O(1)
  • case4： i’L == L，重合，i增长， O(n)

可见只有case1 和case4 需要扩，字符串长度为n，则为O(n)

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
// 慎用，string累加时在处理拷贝内存时耗时很大
string manacher_string(const string& s)
{
    string res = "#";
    int len = s.length();
    for (int i = 0; i < len; ++i){
        res = res + s[i] + "#";
    }
    return res;
}

string manacher_string_2(const string& s)
{
    int len = s.size() * 2 + 1;
    string res;
    res.resize(len);
    int idx = 0;
    for (int i = 0; i < len; ++i){
        res[i] = (i&1)==0 ? '#' : s[idx++];
    }    
    return res;
}

int get_max_len_of_sub_str(const string& s)
{
    string manacher_str = manacher_string(s);
    cout << "manacher_str: " << manacher_str << endl;
    int manacher_str_len = manacher_str.length();
    cout << "manacher_str_len: " << manacher_str_len << endl;
    int pArr[manacher_str_len];  // 回文数组，记录该位置的回文子串R是多大
    int C = -1;
    int R = -1;
    int max_range = INT_MIN;
		/**
     * pArr[i] = R > i ? min(pArr[2*C - i], R - i) : 1;
     * 该行对case1 case2 case3进行了整合, 确定了起码的回文半径
     * 分析case1时，i 在 R 的右边，则R > i 不成立，pArr[i] = 1,则: 
     *      (i+1 < len) && (i-1 > -1) 条件成立，进入while向右扩
     * 分析case2 和 case3时，知道扩不动，时间复杂度O(1)，然后再尝试扩一下，时间复杂度也是O(1)
     *      取i位置对称点i'的最大回文半径pArr[2*C-i] 和[i, R]这段的最小值为pArr[i]
     *      进入while第1下就break，因为明确的知道 i+pArr[i] 处字符一定不等于 i-pArr[i]处字符
     */
    for (int i = 0; i < manacher_str_len; ++i){
        pArr[i] = R > i ? min(pArr[2*C - i], R - i) : 1;
        while (i + pArr[i] < manacher_str_len && i - pArr[i] > -1){
            if (manacher_str[i + pArr[i]] == manacher_str[i - pArr[i]]){
                pArr[i]++;
            }
            else{
                break;
            }
        }
        if (i + pArr[i] > **R){
            R = i + pArr[i];    // R是最大回文子串的长度，不是字符串的下标
            C = i;
        }
        max_range = max(max_range, pArr[i]); // 记录一个最大的回文长度
    }
    return max_range - 1;
}