KMP

 2021-09-25 /  ryanxw

1. 概念

KMP算法的用处是为了加快子串match_str在母串orign_str中匹配查找的过程，如果匹配到则返回match_str在orign_str中的下标位置，如果没有则返回-1。

如果假设母串的长度是N，子串的长度是M，则可以看出时间复杂度的差距之大：
- 暴力解法：O(N*M)
- KMP解法：O(N)

2. 实现原理

既然想知道KMP算法优化了哪里，首先要知道常规的暴力解法慢在哪里，这样才能搞明白为什么KMP真正的进行性能提升。

假设现在有母串orign_str和子串match_str

orign_str = “1234abc1234defk1234abc1234xyz789”

match_str= “1234abc1234xyz”

2.1 暴力解法

所谓暴力匹配就是从左到右一个一个字符的匹配，相同就都向后跳；一旦不同，子串从头开始和母串上一次的下一个字符开始匹配重复之前的过程直到结束。

时间复杂度：O(M*N)

上述的例子：

开始 origin_str[i++] 和 match_str[j++] 进行比较，直到字符d≠x停止
接着 origin_str[1] 和 match_str[0] 再进行比较，不相等
接着 match_str[2] 和 match_str[0] 再进行比较，不相等
…..
match_str[7] 和 match_str[0] 相等，直到字符d≠a停止
接着match_str[11] = ‘d’ 接着和 match_str[0] 比较，不相等
接着match_str[12] = ‘e’ 接着和 match_str[0] 比较，不相等
…..
match_str[15] 和 match_str[0] 相等，直到子串匹配完成，返回母串下标idx = 15

根据上述的简易流程可以明显看出冗余许多无效匹配，这正是KMP进行优化的地方。

2.2 KMP解法

2.2.1 基础知识：字符串的最大前缀，最大后缀

最大前缀：不包含最后一个字符
最大后缀：不包含第一个字符

例子：str = “123b”，对于b这字符的最大前缀是“12”，最大后缀是“23”

2.2.2 next数组：用于KMP优化的核心点

定义：是根据子串建立的数组，表达的是最大前缀和最大后缀二者相匹配的长度
人为规定：
- next[0] = -1
- next[1] = 0

例子：字符串str1 = “aaaab”，则next[5] = {-1, 0, 1, 2, 3}

2.2.3 KMP是如何加速了匹配流程的呢？

继续使用之前的例子：

orign_str = “1234abc1234defk1234abc1234xyz789”，指针p1

match_str= “1234abc1234xyz”，指针p2

当第一次匹配到 d ≠ x 时，需要做下面的事情：
- 根据 match_str 的 next 数组 x 字符所处下标的 next 数组值为4
- p2指针跳转到 match_str[4] 处继续和 orign_str 中的d字符进行匹配
  - match_str[4] ≠ ‘d’，则需要p2指针继续根据 next 数组向前跳转到 p2 = next[4] = 0 进行匹配
  - match_str[0] = “1” ≠ ‘d’，此时 next[p2] = -1，表示子串的第一个字符都已经和’d’字符不相等了，则母串的指针p1只能是继续右移了

以上过程就是加速的过程，保证了母串的指针p1不会向前跳转，一直向后增长，时间复杂度降到O(N)。

代码实现：

int get_index(const string& orign_str, const string& match_str) {
    int p1 = 0, len1 = orign_str.length();
    int p2 = 0, len2 = match_str.length();
    vector<int> next = get_next_arr(match_str);
    while (p1 < len1 && p2 < len2) {
        if (orign_str[p1] == match_str[p2]) {
            p1++;
            p2++;
        }
        else if (next[p2] == -1) {
            p1++;
        }
        else {
            p2 = next[p2];
        }
    }
    return p2 == len2 ? (p1 - p2) : -1;
}

问题记录

Q1：为什么在X ≠ Y 的时候要将 match_str 中的 Z 去和 X 比较？
X ≠ Y 发生的时候，根据 match_str 的 next 数组可以得知 partA == partB，所以直接舍弃 orign_str 字符串中 J 之前的部分，不再进行比较，直接将逻辑上看着就是直接将 match_str 推送到 orign_str 字符串中 J 位置上，而 partC == partB，则 partA == partC 无需再比较，直接比较X和Z即可。
Q2：为什么可以直接抛弃掉 orign_str 字符串中 J 之前的部分？真的不会匹配出一个 match_str 吗？
假设这段有一个位置K，从此位置开始可以匹配出一个 match_str，则必然 [K, X] 这一段范围的字符串是存在于match_str中的，因为第一次匹配的时候是一路匹配下来的，按照这样则 match_str 的 next 数组值应该区域更大，和现有的发生矛盾，则证明一定可以抛弃。

2.2.4 next数组的求解

前面的next数组的值求取是依赖其位置字符的最大前缀和最大后缀的相同的长度，没有说如何快速生成，一直当作一个黑盒在使用。

其实 i 位置的值是依赖 i-1 位置的值，所以根据下图得知：

求取 i 位置的值，只需要判断 b 的 next[] 值的下一个字符即？是否和字符 b 相等即可

相等，则next[a] = next[b] + 1
不等，则前推；若一直推到 index = 0 处还没有相等的，则为 0

vector<int> get_next_arr(const string& match_str)
{
    int len = match_str.length();
    vector<int> next;
    next.assign(len, 0);
    next[0] = -1;
    next[1] = 0;
    int cn = 0;
    int i = 2;
    while (i < len){
        if (match_str[i - 1] == match_str[cn]){
            next[i++] = ++cn;
        }
        else if (cn > 0){
            cn = next[cn];
        }
        else{
            next[i++] = 0;
        }
    }
    return next;
}

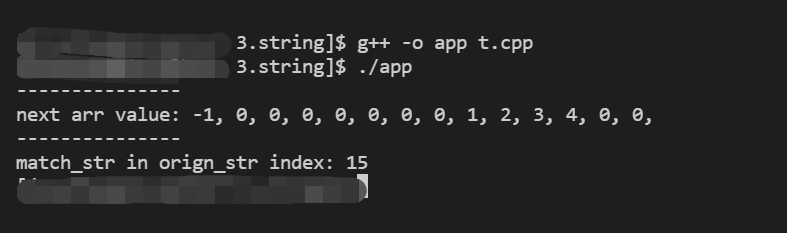
2.2.5 完整代码测试

#include <iostream>
#include <vector>
using namespace std;

vector<int> get_next_arr(const string& match_str)
{
    int len = match_str.length();
    vector<int> next;
    next.assign(len, 0);
    next[0] = -1;
    next[1] = 0;
    int cn = 0;
    int i = 2;
    while (i < len){
        if (match_str[i - 1] == match_str[cn]){
            next[i++] = ++cn;
        }
        else if (cn > 0){
            cn = next[cn];
        }
        else{
            next[i++] = 0;
        }
    }
    return next;
}

int get_index(const string& orign_str, const string& match_str) {

    int p1 = 0, len1 = orign_str.length();
    int p2 = 0, len2 = match_str.length();
    vector<int> next = get_next_arr(match_str);
    cout << "---------------\n";
    cout << "next arr value: ";
    for (int i = 0; i < next.size(); ++i) {
        cout << next[i] << ", ";
    }
    cout << "\n---------------\n";
    while (p1 < len1 && p2 < len2) {

        if (orign_str[p1] == match_str[p2]) {
            p1++;
            p2++;
        }
        else if (next[p2] == -1) {
            p1++;
        }
        else {
            p2 = next[p2];
        }
    }
    return p2 == len2 ? (p1 - p2) : -1;
}

int main()
{
    string orign_str = "1234abc1234defk1234abc1234xyz789";
    string match_str = "1234abc1234xyz";
    int index = get_index(orign_str, match_str);
    cout << "match_str in orign_str index: " << index << endl;
    return 0;
}

测试结果：