常见排序算法总结
2021-09-13 / ryanxw

本文介绍的几种排序算法的时间复杂度、额外空间复杂度、稳定性如下：

排序算法 平均时间复杂度 额外空间复杂度 稳定性
bubble O(n^2) O(1) yes
insert O(n^2) O(1) yes
select O(n^2) O(1) no
merge O(n*logn) O(n) yes
heap O(n*logn) O(1) no
quick O(n*logn) O(n*logn) no

稳定性概念：保证集合中的元素在排序后的相对次序和排序前为一致则是稳定的。例子如下：

1
2
3
原始顺序：[a1, b1, a2, a3, c5]
排序顺序：[a1, a2, a3, b1, c5]
其中三个a类型的相对次序没有发生变化则表示是稳定的。

1. bubble sort

  • 原理：每一轮将该集合的元素中最大的一个沉底即可。
  • 例子：
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    [7, 6, 8, 3, 1, 0]
      第1轮：实现将最大的8放到最后一个位置
      [7, 6, 8, 3, 1, 0] ->
      [6, 7, 8, 3, 1, 0] ->
      [6, 7, 3, 8, 1, 0] ->
      [6, 7, 3, 1, 8, 0] ->
      [6, 7, 3, 1, 0, 8]
      
      第2轮：实现将最大的7放到倒数第2个位置
      [6, 7, 3, 1, 0, 8] ->
      [6, 3, 7, 1, 0, 8] ->
      [6, 3, 1, 7, 0, 8] ->
      [6, 3, 1, 0, 7, 8]

      以此类推，若集合的大小是n，则需要进行n轮，每轮比较n次
      则时间复杂度为O(n^2)
  • 实现： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    void bubbleSort(int a[], int len){
        for (int i = 0; i < len; ++i){
            for (int j = 0; j < len - i - 1; ++j){
                if (a[j] > a[j + 1]){
                    swap(a[j], a[j + 1]);
                }
            }
        }
    }

2. insert sort

  • 原理：将index = 0的位置看作是一个有序区，之后将后续的元素按照大小插入到有序区对应的位置即可。
  • 例子： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    [7, 6, 8, 5, 1, 0]
        第1轮：[7]是有序区
        [7, 6, 8, 5, 1, 0] ->
        [6, 7, 8, 5, 1, 0]
        
        第2轮：[6, 7]是有序区
        [6, 7, 8, 5, 1, 0] ->
        [6, 7, 8, 5, 1, 0]

        第3轮：[6, 7, 8]是有序区
        [6, 7, 8, 5, 1, 0] ->
        [6, 7, 5, 8, 1, 0] ->
        [6, 5, 7, 8, 1, 0] ->
        [5, 6, 7, 8, 1, 0]

        以此类推，若集合的大小是n，则需要进行n轮，
        比较的次数是一个等差数列的和，则时间复杂度为O(n^2)
  • 实现： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    void insertSort(int a[], int len){
        for (int i = 1; i < len; ++i){
            for (int j = i - 1; j >= 0; --j){
                if (a[j] > a[j + 1]){
                    swap(a[j], a[j + 1]);
                }
            }
        }
    }

    3. select sort

  • 原理：从元素中找出最小的数放到集合的index=0的位置，之后轮询n次每次将最小的数放到有序集合后面即可。
  • 例子： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    [7, 6, 8, 5, 1, 0]
        第1轮：选择最小的元素0放到起始位置
        [7, 6, 8, 5, 1, 0] ->
        [6, 7, 8, 5, 1, 0] ->
        [5, 7, 8, 6, 1, 0] ->
        [1, 7, 8, 6, 5, 0] ->
        [0, 7, 8, 6, 5, 1] 
        
        以此类推，若集合大小是n，则需要进行n轮，
        比较的次数是一个等差数列的和，则时间复杂度为O(n^2)
  • 实现： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    void selectSort(int a[], int len){
        for (int i = 0; i < len; ++i){
            for (int j = i + 1; j < len; ++j){
                if (a[j] < a[i]){
                    swap(a[j], a[i]);
                }
            }
        }
    }

    4. merge sort

  • 原理：不停的将集合二分（逻辑上的划分），直到元素不能再划分为止，则申请对应的空间按相对大小填充返回即可。
  • 例子： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    [2, 1, 4, 5, 3, 6]
        第1轮：以 index = 2 开始划分
        [2, 1, 4]  [5, 3, 6]

        第2轮：将第1轮的集合左右各自继续划分
        [2, 1] [4] [5, 3] [6]

        第3轮：将第2轮中可以划分的继续划分
        [2] [1] [4] [5] [3] [6]

        第4轮：按照划分好的结果通过大小逆序向上合并填充即可
        [1, 2] [4] [3, 5] [6] ->
        [1, 2, 4] [3, 5, 6] -> 
        [1, 2, 3, 4, 5, 6]
  • 实现： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    void mergeSort(int a[], int l, int r){
        if (l == r) return;
        int mid = l + (r - l) / 2;
        mergeSort(a, l, mid);
        mergeSort(a, mid + 1, r);
        merge(a, l, mid, r);
        return;
    }
    void merge(int a[], int l, int mid, int r){
        int len = r - l + 1;
        int help[len];
        int help_idx = 0;
        int p1 = l;
        int p2 = mid + 1;
        while (p1 <= mid && p2 <= r){
            help[help_idx++] = a[p1] < a[p2] ? a[p1++] : a[p2++];
        }
        while (p1 <= mid){
             help[help_idx++] = a[p1++];
        }
        while (p2 <= r){
             help[help_idx++] = a[p2++];
        }
        for (int i = 0; i < len; ++i){
            a[l + i] = help[i];
        }
        return;
    }
  • 应用：
    • 小和问题：每个位置上左边有比该位置值小的所有的数的和。
      1
      2
      3
      4
      5
      6
      7
      [2, 1, 4, 5, 3, 6]
      small_sum = (2 + 1) + 
                  (2 + 1 + 4) + 
                  (2 + 1) + 
                  (1 + 2 + 3 + 4 + 5)
      在 merge 的过程中就可以计算出所有小和
      a[i] < a[j] 则出现的次数总和为：(r - j + 1) * a[i]
    • 逆序对：每个位置右边有比该位置数小的数对个数。
      1
      2
      3
      4
      5
      6
      7
      [2, 1, 4, 5, 3, 6]
      逆序对个数：
      [2, 1]
      [4, 3]
      [5, 3]
      在 merge 的过程中可以求取逆序对个数：
      a[i] > a[j] 则逆序对的个数为：(mid - i + 1)

      5. heap sort

  • 原理：堆排的实现对应算法中的优先级队列，核心分为2步：建堆和调堆

    • 建堆：通过比较当前位置的树是否比起父节点大的方法来创建一个大根堆（以该节点为根的树是该节点是最大值）。建堆只需要在数组上调整即可，逻辑上对应的是一棵完全二叉树，时间复杂度为O(n)。
      关注两点：

      父节点index = i，左右孩子节点left = 2*i + 1, right = 2*i + 2；
      孩子节点index = i，父节点fa = (i - 1) / 2

    • 调堆：将堆的根节点调到最后一个叶子节点处（即数组的最后一个位置），剪枝，之后从根节点进行元素调整继续维护为一个大根堆的样子便于下次取到最大值元素，该操作的时间复杂度为O(n*logn)

  • 例子： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    [4, 0, 5, 3, 1, 2, 7]

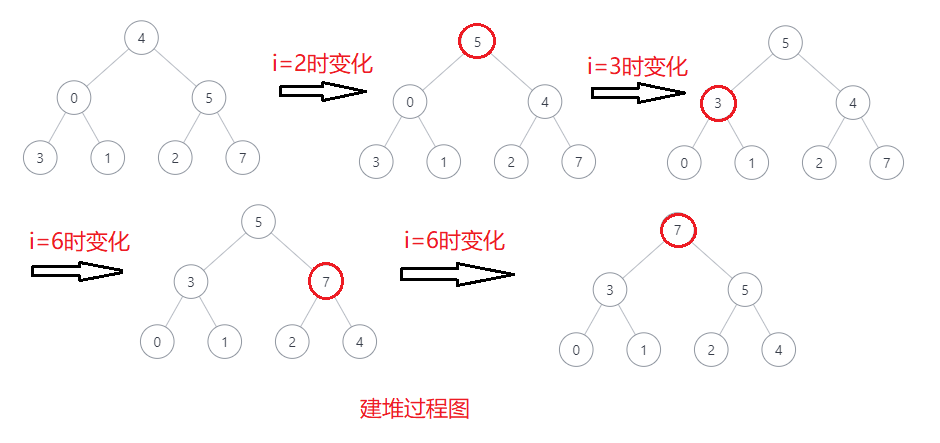
    step1: 建堆，判断当前位置的数是否比其父亲节点大，若大则交换，则index从0到N扫描，第i个节点树的高度为log(i)
    则T(N) = log(1) + log(2) + ... + log(N) 可以在O(N)内收敛
    [4, 0, 5, 3, 1, 2, 7] ->
    [5, 0, 4, 3, 1, 2, 7] ->
    [5, 3, 4, 0, 1, 2, 7] ->
    [7, 3, 5, 0, 1, 2, 4]

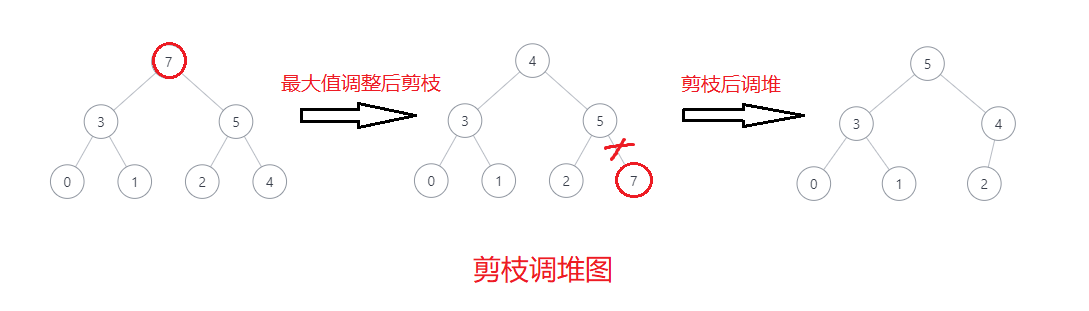
    step2: 调堆 O(N * logN)
    将7置换到数组末尾进行剪枝后再进行调堆
    [7, 3, 5, 0, 1, 2, 4] ->
    [4, 3, 5, 0, 1, 2, (7)] ->
    [5, 3, 4, 0, 1, 2, (7)]

    以此类推直到取完最后一个节点为止即可
  • 例子示例图：
    • 建堆图：
    • 剪枝调堆图：
  • 实现：
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    void heapSort(int a[], int len){
        if (len <= 1) return;
        for (int i = 0; i < len; ++i){
            heapInsert(a, i);
        }
        int size = len;
        swap(a[0], a[--size]);
        while (size > 0){
            heapify(a, 0, size);
            swap(a[0], a[--size]);
        }
    }
    void heapInsert(int a[], int index){
        while (a[index] > a[(index - 1) / 2]){
            swap(a[index], a[(index - 1) / 2]);
            index = (index - 1) / 2;
        }
        return;
    }
    void heapify(int a[], int index, int size){
        int left = index * 2 + 1;
        while (left < size){
            int largest = left + 1 < size && a[left + 1] > a[left] ? left + 1 : left;
            largest = a[largest] > a[index] ? largest : index;
            if (largest == index){
                break;
            }
            swap(a[largest], a[index]);
            index = largest;
            left = index * 2 + 1;
        }
        return;
    }

    6. quick sort

  • 原理：核心partition过程来将数组按照随机选定一个值p将元素划分为<p, =p, >p三个区域，将等于区域返回之后继续递归划分直到不能划分结束。
    • 随机选定元素的原因：从规模上减少每次选择的划分值不好，增大递归的规模，从而使时间复杂度退化为O(n^2)。
    • 递归划分时每次都选择中间值，则递归规模每次为n/2，根据master公式可以得知T(N) = 2 * T(N / 2) + O(N^1)，则时间复杂度收敛到O(N*logN)。
  • 例子：
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    [7, 6, 8, 4, 5, 2, 0]
      step1: 假设随机选取划分值p = 4
      step2: partition过程，根据p = 4进行划分，该过程时间复杂度O(N)
          a[i] < p 时则小于区域扩大，小于区的下一个元素和a[i]交换，同时i自增
          a[i] = p 时则等于区扩大，i自增
          a[i] > p 时则i保持不变，大于区前一个数和a[i]交换，大于区扩大
        [7, 6, 8, 4, 5, 2, 0] ->
        [0, 6, 8, 4, 5, 2, 7] ->
        [0, 2, 8, 4, 5, 6, 7] ->
        [0, 2, 5, 4, 8, 6, 7] ->
        [0, 2, 5, 4, 8, 6, 7]

      step3：将partition过程等于区域的index数组[3, 3]返回用于下一次递归即可

      额外空间复杂度 O(N*logN)，用于保存partition过程中树的节点
  • 实现：
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    void quickSort(int a[], int l, int r){
        if (l < r){
            int r_index = l + rand() % (r - l + 1);
            swap(a[r_index], a[r]);
            int *parr = partition(a, l, r);
            quickSort(a, l, parr[0] - 1);
            quickSort(a, parr[1] + 1, r);
        }
        return;
    }
    int* partition(int a[], int l, int r){
        int less = l - 1;
        int more = r;
        int *parr = new int[2];
        int m = l;
        while (m < more){
            if (a[m] < a[r]){
                swap(a[++less], a[m++]);
            }else if (a[m] == a[r]){
                m++;
            }else{
                swap(a[m], a[--more]);
            }
        }
        swap(a[r], a[more]);
        parr[0] = less + 1;
        parr[1] = more;
        return parr;
    }
  • master公式普及
    1
    2
    3
    4
    T(N) = a * T(N / b) + O(N^d)
    (1) logb(a) = d 则 T(N) = N^d * logN
    (2) logb(a) > d 则 T(N) = N^logb(a)
    (3) logb(a) < d 则 T(N) = N^d